Axis of Beam (or Centroidal axis). It is a line passing through centroids of all cross-sections of the beam. Line EF is the axis of beam.
Axis of Symmetry. It is a line about which the area of cross-section of the beam is sy mrnetrical. For example, circular, rectangular and square sections have two axes of symmetry, where as T- and I-sections have only one axis of symmetry. AC, BD, CL and HK are the axes of symmetry.
Plane of Symmetry. It is a plane passing through the axis of symmetry. GHKL is the plane of symmetry.
Plane of Bending. It is a plane in which bending takes place. For vertical loading, the plane of symmetry and plane of bending coincide. GHKL is the plane of of bending.
Neutral Surface. It is a surface on which the bending stress is zero ar d the beam fibres do not undergo any tension or compression. ABDC is the neutral surface.
Neutral Axis. It is a line where the neutral surface intersects with the area of cross- section of the beam. AC and BD are the neutral axes.
Centroid : The centroid of a plane area is that point at which the whole of the area of the plane may be assumed to be concentrated. If a plane area is subdivided into small areas A1, A2 ,and the perpendicular distances of the centroids of these areas from two chosen coordinate axes and y are y1, Y2 , and x1, x2, respectively, then the coordinates of the centroid (, ) of the whole area are given by:
Moment of Inertia. The moment of inertia or the second moment of area of a plane figure about a given axis is the sum of the product of the elementary areas into which plane figure may be divided and the square of the distance of the centroids of elementary areas from the chosen axis. Thus
Parallel Axis Theorem. This theorem states that the moment of inertia of a plane figure about any axis in its plane, is equal to the total sum of the moment of inertia of the fig’ure about a parallel axis through the centroid of the figure plus the product of the total area of the figure and the square of the distance between the parallel centroidal axis and
the axis of reference.
For example,




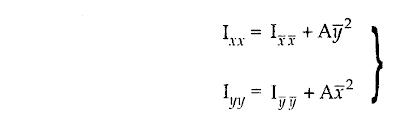
No comments:
Post a Comment